Re-basing GDP and Estimating Growth Rates

NOTE: The Growth Economics Blog has moved sites. Click here to find this post at the new site.

Leandro Prado de la Escosura recently posted a voxeu column about splicing real GDP series after re-basing. Re-basing of real GDP means adopting a new set of reference prices to value output in each year. Think of what Nigeria did last year, when they re-based from 1990 prices to using 2010 prices, and all of the sudden measured real GDP was about twice as big.

de la Escosura’s point is that when we re-base and “retrocast” real GDP numbers to past years, we may obscure evidence of rapid economic growth. You should go read his post, and his associated paper, to understand his point in full. But let’s use the Nigerian 2013 re-basing to get the basic idea. Let’s say that in 1990 Nigeria produced 1000 units of food, and zero motorcycles. In 2010 Nigeria produced 1000 units of food again, but produced 200 motorcycles. So there clearly is real growth in output.

In 1990, the price of food was 1 naira per unit and motorcycles were 500 naira. 1990 real GDP in 1990 prices is 1000(1) + 0(500) = 1000. 2010 real GDP in 1990 prices is 1000(1) + 200(500) = 101,000. This is a dramatic growth rate of real GDP (10,100% actually).

After re-basing, what do we get? In 2010 the price of food was 2 naira per unit, and motorcycles were 100 naira each. So 1990 real GDP in 2010 prices is 1000(2) + 0(100) = 2000. 2010 real GDP in 2010 prices is 1000(2) + 200(100) = 22,000. Still a lot of growth, but only 1100%. The growth rate of real GDP between 1990 and 2010 went from over 10,000% to about 1100%, an order of magnitude drop. Growth looks much slower in Nigeria after re-basing.

Why? Because with dramatic economic growth came dramatic changes in relative prices. Motorcycles dropped severely in price, while food went up slightly. Combined, this makes food look more valuable compared to motorcycles by 2010. So valuing 1990 output in 2010 prices tends to make 1990 look pretty good, because in 1990 they had lots of food relative to motorcycles.

de la Escosura’s argument is that in 1990, for sure, the 1990 prices are the right way to value real GDP. Similarly, in 2010, for sure, the 2010 prices are the right way to value real GDP. So leave those years priced in their own prices. For the nineteen intervening years, 1991-2009 inclusive, compute their real GDP in both 1990 and 2010 prices. Then average those two estimates depending on how far from each year we are.

So for 1991, let real GDP be (1991 GDP at 1990 prices)(18/19) + (1991 GDP at 2010 prices)(1/19). For 1992, let real GDP be (1992 GDP at 1990 prices)(17/19) + (1992 GDP at 2010 prices)(2/19), and so forth. For de la Escosura, this better captures the growth in real GDP over time. For our example, 1990 real GDP in 1990 prices is 1000, and 2010 real GDP in 2010 prices is 22,000, and the growth rate is 2,200%. It essentially splits the difference of the two different benchmarks, preserving some of the rapid growth seen using the 1990 prices.

This isn’t necessarily a new concept. Johnson, Larson, Papageorgiou, and Subramanian discuss this issue in their paper on the Penn World Tables. Their suggestion for a chained PWT price index amounts to a similar suggestion.

The big point is that by re-basing you are necessarily screwing with the implied growth rate of real GDP because you are screwing with the value of real GDP in the first year (1990 in our example). If there has been a lot of economic growth and relative prices have changed, then almost certainly the first year will have a higher measured real GDP when we re-base. With a higher initial level of GDP, the growth rate will necessarily be smaller.

If your worry about computing growth rates, then this is an issue you have to worry about a lot, and something like de la Escosura’s method or the Johnson et al suggestion is what you should do. If you worry about comparing income levels across countries, then this critique is not crucial (although you have other things to worry about).

What does Real GDP Measure?

NOTE: The Growth Economics Blog has moved sites. Click here to find this post at the new site.

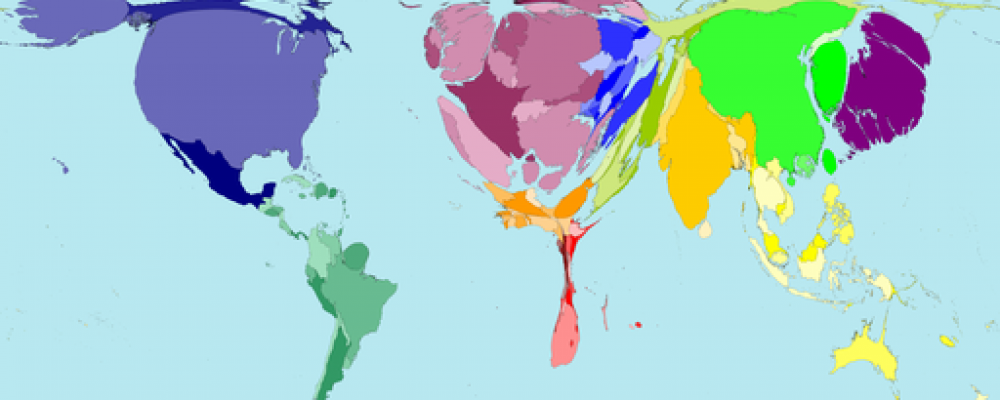
Nearly all cross-country work on growth and development uses, if only for motivation, Penn World Table (PWT) estimates of real GDP for countries. And the PWT generates a single measure of “real GDP” for each country. How do they do this? Before I answer, let me say that much of what I’m going to say is said more thoroughly in Deaton and Heston (2010). So check that out if you’re into cross-national real GDP comparisons.

To start, let’s simplify and think just about two countries, A and B. To compare real GDP in the two countries, we’d want to value the quantities of goods they produce at some common set of prices. So say phones are $50, and haircuts are $10, and then for each country multiple the quantitify of phones times 50 and add the quantity of haircuts times 10. But what are the right prices to use? Why 50 and 10? Why not 60 and 5? You can imagine that we want the prices we use to be somewhat meaningful, and at least related to the observed prices in countries.

So here’s where it gets weird. We could say, whatever, let’s just use the prices from country B. I just need to pick one set of prices, right? But if you measure country A’s GDP using country B’s prices, then country A will look relatively rich compared to country B. This doesn’t mean it makes country A look absolutely richer than country B, just that country A now looks better in comparison. This works if you flip them around. If you measure country B’s GDP using country A’s prices, then country B will look relatively rich compared to country A. This isn’t a mathematical certainty, but reflects what actually happens if you use the prices underlying the PWT.

Let’s take the U.S. and Nigeria as an example. If we measure real GDP in both the US and Nigeria using Nigerian prices, then the US will appear to have an incredibly large lead over Nigeria in GDP per capita. If we measure real GDP in both the US and Nigeria using US prices, then the gap will appear smaller as this will make Nigeria look particularly good.

This doesn’t necessarily have to happen, it’s not some mathematical rule. But the data underlying the Penn World Tables shows that this is the case almost universally. So what is going on? It means that country A has (relatively) high prices for what country B has a lot of, and country A has (relatively) low prices for what country B has little of.

It’s easiest to see this in an example. So let the US produce and 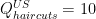. The US produces a lot of phones relative to haircuts. And in the US, and , or haircuts and phones cost the same. [No, this doesn’t have to be a realistic relative price for this to work]. At US prices, real GDP in the US is

In Nigeria, we have and , or Nigeria has very few phones, but lots of haircuts. And the prices in Nigeria reflect this, with 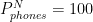and . At Nigeria’s prices, real GDP in Nigeria is

Now, those two numbers are not comparable because they use different absolute prices to value the goods. To do a fair comparison of output in the two countries, we have to use the same prices.

Let’s value Nigeria’s output using the US prices

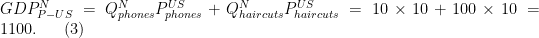
So using US prices, Nigeria looks really good. Their GDP is 1100, exactly equal to the US. They achieve this with lots of haircuts and few phones, so utility could be different in the two places, but their measured real GDP is as high as the US.

But we could equally argue that we should use Nigerian prices to value GDP in both countries. So for the US we get

The US now has GDP of 10,100, while Nigeria (at its own prices) only has a GDP of 2000. The US is roughly 5 times richer than Nigeria, when valued at Nigerian prices. Why? Because the US produces a lot of what Nigerians find expensive (phones), and little of what they don’t (haircuts).

Which comparison is right? Neither. There is nothing that says we should use the US prices or the Nigerian prices. For real GDP we simply need to pick some set of prices, and use them consistently across all countries. So much of the work in the Penn World Tables is to come up with a common price index. And the nature of this singular set of prices will matter a lot for real GDP comparisons. If the PWT uses prices that look alot like US prices, then this will make Nigeria (and other developing countries) look relatively well off compared to rich countries. But if the PWT used prices that look like Nigerian prices, then this will exaggerate the gap.

In practice, what do they do? They try to construct some kind of weighted average of the price of each good across all countries. The weights are in the PWT are calculated using what is called a Gheary-Khamis method, which essentially weights the prices from different countries by their share of total spending on that good. For phones, the weight for the U.S. is because they produce/use 91% of all the phones. For haircuts, the weight for the U.S. is because they produce/use about 9% of all haircuts.

Now in my simple example the weights are basically symmetric, because the US has most of the phones, and Nigeria has most of the haircuts. But in the real data, the US has far more phones and more haircuts than Nigeria. So in practice in the PWT, the weights are very large on U.S. prices, and very small on Nigerian prices. When they do these calculations across all countries, the weights on the US, Western Europe, and Japan dominate because they consume most of the stuff out there in the world. So the prices used by the PWT are really similar to a relatively rich Western nation [People have argued that the prices roughly correspond to Italy’s].

Which all means that every country in the PWT is getting valued at rich country prices. As we saw above, this inflates the real GDP of very poor countries, and makes them look “good” compared to rich countries. That is, the gap between the U.S. and Nigeria is much smaller using rich country (e.g. US) prices than Nigerian prices. So the PWT overall makes poor countries look very good. The true gaps in real GDP are likely larger (much larger?) than what the PWT captures.

This is not some kind of deliberate subterfuge by the PWT. “It does what it says on the tin” is a phrase that comes to mind. But that doesn’t mean it has some cosmic truth to it. The PWT isn’t doing anything wrong, but they are running up against the real fundamental problem: there is no set of prices that gives us a true measure of real living standards across countries.

What we’d like is some number that tells us that living standards in Nigeria are one-tenth, or one-twentieth, or one-fifth of those in the U.S. But what do you mean by living standards? No measure of real GDP captures actual welfare. Even if – as we’d assume was the case in a perfectly competitive market – relative prices capture relative marginal utilities, real GDP doesn’t measure welfare.

Multiplying the total quantity times the marginal utility of a good doesn’t tell me anything about the total utility that people enjoy from that good. The marginal utility of a 3rd car in my family is essentially zero, but that doesn’t mean that we get no utility from having 2. So even if there were some “right” set of prices we could use to value real GDP, it still wouldn’t measure welfare.

I think what would be useful for the PWT would be to have the full distribution of real GDP estimates for a country. That is, show me Nigeria’s real GDP valued at the prices found in every single other country in the PWT. I could plot that distribution of real GDP’s in Nigeria against the same distribution of real GDP’s for the U.S. This would at least show me something about the noise in the relative standing in real GDP for these countries. This sounds like something I can make a grad student do.

One last note about these comparisons. Recall that the result that measuring country A’s GDP in country B’s prices makes country A look relatively rich is not a certainty. It holds because there is a specific correlation of prices and quantities in the data. In each country, goods that are produced in large quantities (e.g. haircuts in Nigeria) tend to have low relative prices, and goods produced in small quantities (e.g. phones in Nigeria) tend to have high relative prices. In other words, price and quantity are negatively related. This implies that the main differences between countries are supply differences, not demand differences.

If Nigeria didn’t have a lot of phones because Nigerians didn’t like phones, then phones in Nigeria would be cheap compared to haircuts. And then valuing Nigeria’s output at the U.S. prices, which also has cheap phones compared to haircuts, wouldn’t make Nigeria look so rich. It might make them look poorer, in fact. So the empirical fact that valuing Nigeria’s output at U.S. prices makes Nigeria look relatively rich is evidence that Nigeria and the U.S. have different supply curves for phones and haircuts, not different demand curves [Yes, demand is probably different too. But relative to supply differences, these appear to be small].

Measuring Real GDP

NOTE: The Growth Economics Blog has moved sites. Click here to find this post at the new site.

This morning Angus Deaton and Bettina Aten released an NBER working paper (gated, sorry) about understanding changes to international measures of real GDP and poverty that occurred following the release of a new round of price indices from the International Comparison Project (ICP).

Price indices? Methodological nuance? I know, ideal subject matter to drive my web traffic to zero.

For those of you still here (thanks mom!), the paper by Deaton and Aten is a great chance to understand where comparisons of real GDP across countries come from, and to highlight that these comparisons are inherently imprecise and should be used with that in mind.

The basic idea of the Penn World Tables, or any other attempt to measure real GDP across countries, is to compute the following

where is the real GDP number we want, is the nominal GDP reported by a country, and is the “purchasing-power-parity” price index for that country. While there can be severe issues with the reporting of nominal GDP, particularly from poor countries with a bare-bones (or no) national statistics office, the primary concern in these calculations is with the .

Think of as the cost of one “bundle of goods” in country . So dividing nominal GDP by gives us the number of real bundles that a country produced. If we do that for every country, we can compare the number of real bundles produced across countries, and that crudely captures real GDP.

The ICP produces these measures of for each country. I’m going to avoid the worst sausage-making aspect of this, because it involves lots of details about surveys to find prices for specific goods, how to get the right “average” price for each good, and then how to roll those back up to for each country. The important thing about the methodology for computing is that there is no right way to do it. There are methods that might be less sensible (i.e. let be the price of a can of Diet Coke in a country) than what the ICP does, but that doesn’t imply that the ICP is correct in some absolute sense.

It also means that the ICP can, and does, change methodology over time. The paper by Deaton and Aten works through the changes in methodology from 1993/5 to 2005 to 2011 and how we measure real GDP. The tentative conclusion is that the 2005 iteration of the ICP probably was over-stating the levels for many developing African and Asian countries. From the equation above, you can see that over-stating the means under-stating real GDP. So in 2005, we were likely too pessimistic about the economic conditions in a lot of these developing countries. Chandy and Kharas found that using the 2005 values of implied that 1.215 billion people in 2010 lived below the World Bank’s $1.25 per day poverty line. Using the 2011 values of instead, there are only 571 million people living below $1.25 per day. That’s a reclassification of some 700 million people. Their domestic income stayed the same, but the 2011 ICP suggests that they were paying lower prices for their “bundle of goods” than we assumed in 2005, and hence their real income went above $1.25.

But as I said before, these are tentative conclusions because there is no way of knowing this for sure. Deaton and Aten’s conclusion is that the 1993/5 and 2011 rounds of the ICP seem more consistent with each other, and 2005 looks like an outlier. So just to keep things comparable over time, we should probably avoid the 2005 numbers. But again, who knows. It’s quite possible that mankind’s true welfare is measured in the number of cans of Diet Coke that we can produce.

Measuring real GDP or global poverty levels is – to put it kindly – a fuzzy process. There is not the right method for this. As you can see, the measurements can be pushed around a lot by differences in methodology that are inherently trying to make apples-to-oranges comparison (I mean that literally – how do you value apples compared to oranges in national output? What’s the right price? It’s different in Washington, Florida, and Wisconsin. So how do you compare the total “real” value of fruit consumption in different states or countries?).

The implication is that we shouldn’t be asking real GDP measures or poverty line measures to do too much. For really crude comparisons, real GDP from the Penn World Tables is fine. The U.S. has higher real GDP per capita than Kenya, and the Penn World Tables pick that up. Is it a 40/1 ratio? A 35/1 ratio? A 20/1 ratio? Not entirely clear. Different methodologies for computing in the US and Kenya will yield different results. But is it really important if it is 40/1 versus 20/1? In either case, it is clear that Kenya is poorer. We can go forth and try to explain why, or make some policy advice to Kenya to help close the gap, or go to Kenya to work on interventions to alleviate poverty there.

Where these real GDP comparisons, or poverty line counts, should not be used is in finer-grain comparisons. Is Kenya’s real GDP per capita lower or higher than Lesotho’s? According to the Penn World Tables, in 2011 Kenya’s was lower. But should we do any kind of serious analysis based on this? No. The difference is as likely to be from discrepancies in how we measure for those countries as from real economic differences in capital stocks, human capital, technology, or institutions.

Real GDP comparisons are best thought of as similar to baseball stats. The top career OPS (on-base plus slugging percent) players are Babe Ruth, Ted Williams, Lou Gehrig, Barry Bonds, and other names you might recognize. Players like Albert Pujols and Miguel Cabrera are in the top 20, giving you a good idea that these guys are playing at a level similar to the greats of all time. You can’t use this career OPS to tell me that Pujols is definitively better than Stan Musial or definitively worse than Rogers Hornsby. But career OPS does make it clear that Pujols and Cabrera are definitely better than guys like Davey Lopes, Edgar Renteria, and Devon White (and distinguishing between Lopes, Renteria, and White is hopeless using OPS).

The fact that ICP revises the values over time doesn’t make them useless, just as OPS isn’t useless even though it ignores defense and steals. But you cannot ask too much of the real GDP measures that are derived using them. They are useful for big, crude comparisons, not fine-grained analysis.